
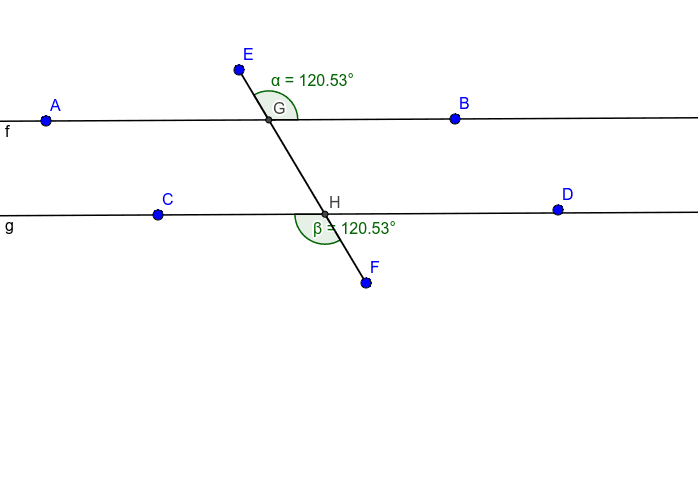
It should be noted that the pair of alternate exterior angles are equal in measure, that is, ∠1 = ∠8, and ∠2 = ∠7 Consecutive Interior Angles In the figure given above, there are two pairs of alternate exterior angles. When two parallel lines are cut by a transversal, the pairs of angles formed on either side of the transversal are named as alternate exterior angles.
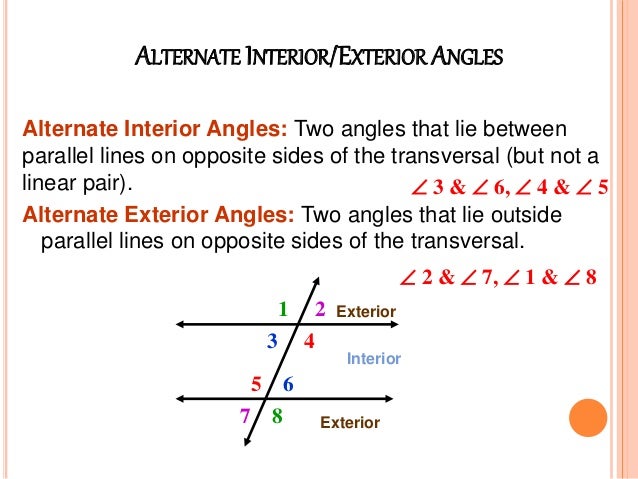
It should be noted that the pair of alternate interior angles are equal in measure, that is, ∠3 = ∠6, and ∠4 = ∠5 Alternate Exterior Angles In the figure given above, there are two pairs of alternate interior angles. It should be noted that the pair of corresponding angles are equal in measure, that is, ∠1 = ∠5, ∠2 = ∠6, ∠3 = ∠7, and ∠4 = ∠8 Alternate Interior AnglesĪlternate interior angles are formed on the inside of two parallel lines which are intersected by a transversal. In the figure given above, the corresponding angles formed by the intersection of the transversal are: When two parallel lines are intersected by a transversal, the corresponding angles have the same relative position. The figure shows two parallel lines 'a' and 'b' which are cut by a transversal 'l'. Observe the following figure to identify the different pairs of angles and their relationship. When parallel lines are cut by a transversal, four types of angles are formed. Angles Formed by Parallel Lines Cut by Transversal


 0 kommentar(er)
0 kommentar(er)
